正则表达式原理探究
正则表达式是被广为使用的工具,功能非常强大,但语法很复杂,想要完全记忆非常麻烦。
偶然间在《算法:第四版》上看到了有关于正则表达式原理的叙述,受益匪浅,在此做下笔记。
正则表达式的定义
**什么是正则表达式?**一个正则表达式对应着一堆字符串,这些字符串构成一个集合,它们的共同特点就是匹配于这个正则表达式。例如:a(a|b) * b 就对应着第一个字符为a,最后一个字符为b,由a和b构成的字符串。
正则表达式有三种核心的基本结构:
- 连接:如 abc,由 a, b, c连接而成。
- 或:如 a|b|c,表示是 a 或 b 或 c。
ab|bcd表示ab或bcd。 - 闭包:如a*b,表示0或若干个a和一个b连接而成的字符串。
以上就是最最最基本的结构,是构成正则表达式的基础。
我们可以使用括号改变优先级顺序,如 c(ac|b)d 表示 cacd, cbd。
至于其它教程里写到的如 +,?, [] 等操作都是基本操作的简略缩写,它们都可以通过基本操作完成。
+ 是由那些基本操作完成的?(文章末尾给出答案)
基本的语法就介绍到这,这篇文章并不是主要讲应用。有兴趣朋友可以在网上搜索完整的语法规则,非常详细。
非确定有限状态自动机
DFA
DFA 又叫确定有限状态自动机,即对于一个输入,它的输出状态是确定的。如图:
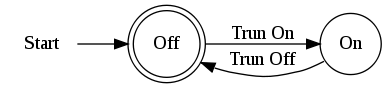
对于这个自动机,输出边是 Turn On 和 Turn Off 的动作,Turn On 导致状态变为 On,Turn Off 导致状态变为 Off。
这两个动作所导致的结果是可以预料的,确定的。所以说是确定有限状态自动机。
NFA
NFA 叫非确定有限状态自动机,和 DFA 的唯一区别是它的输出是非确定的,DFA是NFA的一个子集。如图:
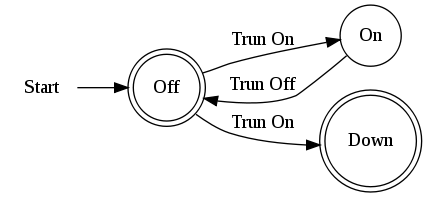
还是那个例子,只不过状态 Off 的 Turn On 操作多了一个新的状态 Down
当我们进行 Turn On 操作时无法确定到达的是 On 还是 Down,因此是无法根据当前状态和输出边确定下一状态的,这就叫做非确定性有限状态自动机。
实例
我们先来看一个示例,它说明了 NFA 的性质和操作。如图:
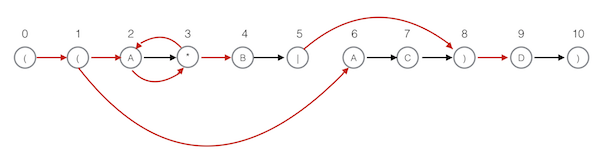
(图表示((A*B|AC)D)所对应的 NFA)
我们定义的NFA有以下特点:
- 正则表达式中每个字符有且只有一个对应的状态。
- 字符所对应的状态有一条指向下一个字符对应状态的边(图中黑色的边)
- “(”, “)”, “|”, 和"*"所对应的状态至少含有一条指出的边,可能指向任意状态(图中红色边)
- 一个状态只能有一条指出的黑色边
我们用构造的NFA去匹配文本,当从起始状态0能够到达最终状态的话,即匹配成功,这就是正则表达式匹配文本的原理。
NFA中状态的转换有以下两种:
- 匹配转换: 当字符匹配时,由黑色的边转换到下一状态。
- ε-转换:不扫描任何字符,通过红色的边转换到另一个状态。
NFA 的运行
运行的核心思想就是:遍历所有可能到达的状态序列,只要其中存在最终状态就匹配成功。类似于动态规划。
首先将NFA中的两个状态转换表示出来。我们用一个char数组re[]保存正则表达式本身 ,如果re[i]存在于字母表中,那么就存在一个从i到i+1的匹配转换。
自然地,ε- 转换就用有向图G表示,实例中的 ε-转换可构建为: 0->1 1->2 1->6 2->3…以此类推。
当处于状态 0 时,我们遍历所有从0通过ε-转换(有向图的深度优先搜索)可到达的状态放入一个集合,再从中查找是否存在最终状态的值。
当匹配一个字符到达状态1后,再遍历所有从1通过ε-转换可到达的状态…如此反复,当文本结束时从集合中找到是否含有最终状态来说明是否到达接受状态。
例如,在实例中初始集合为{1, 2, 3, 4, 6},如果第一个字符为A,则接下来可能的状态为 {3, 7} ,通过 ε- 转换可到 2,4,因此第二个字符状态集合为 {2, 3, 4, 7}。再不断重复这个过程直到文本结束。
输入A A B D会有什么样的轨迹?(文章末尾给出答案)
NFA 的构造
长串的正则表达式都是三个基本操作和括号构成的,因此我们的NFA也可以看作成若干基本操作拼接而成,下面就来介绍一下基本操作所对应的 NFA。
-
连接操作:字符加状态匹配即可。
-
括号:用栈处理。
-
闭包操作:
-
出现在单个字符之后:在该字符和 * 之间添加两条 ε- 转换。
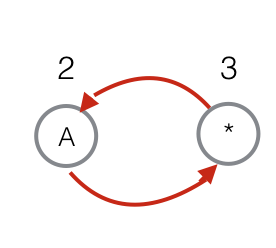
-
出现在右括号之后:在栈顶的左括号和 * 之间添加两条 ε- 转换。
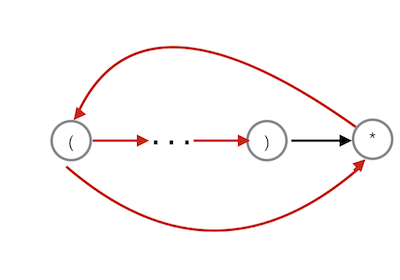
-
-
或:A|B中A和B都是正则表达式。同样也是添加两条ε-转换,一条从左括号指向
B中第一个字符,另一条从|字符指向右括号。这使NFA能够进行选择。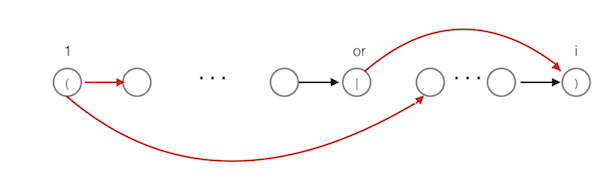
运用以上几个基本的 NFA,我们可以拼接出任意 NFA。
代码
本篇文章以介绍概念为主,具体的实现可参照NFA.java
后记
感想
正则表达式是很强大的工具,网上教程一大把,但多数是直接告诉你语法,基本没规律,只能强记,效率略低。
明白原理后,不仅记忆深刻,而且还可以编写适合自己的规则。
(其实说到底都是《编译原理》课程上的东西,无奈学校不开😤好气哦)
参考资料
- 《算法:第4版》
答案
- + : (ab)+ 等价于 (ab)(ab)*
- {0, 1, 2, 3, 4, 6} -> {2, 3, 4, 7} -> {2, 3, 4} -> {5, 8, 9} -> {10}